Ovatko tuloerot Suomessa kasvaneet luultua enemmän?
Usein väitetään, että tuloerot eivät ole Suomessa enää kasvaneet 2000-luvulla. Väite ei pidä paikkaansa, oli mittarina sitten vuosituloihin tai viiden vuoden keskituloihin perustuvat suhteelliset Gini-kertoimet. Viimeisten reilun kahdenkymmenen vuoden aikana Suomessa tuloerojen suurimmat muutokset ovat tapahtuneet ylimmissä tuloissa. Gini-kerroin, toisin kuin tuloerotutkijoiden suosittelema logaritminen keskiarvopoikkeama eli MLD-mitta, reagoi näihin muutoksiin lievästi. Tuloerot mitattuna MLD-mitalla tai absoluuttisella Gini-kertoimella ovat kasvaneet Suomessa selvästi voimakkaammin kuin on luultu suhteellisen Gini-kertoimen perusteella.
Kirjoittajat kuuluvat Suomen Akatemian Strategisen Tutkimuksen Neuvoston rahoittamaan konsortioon ”Work, Inequality and Public Policy” (No. 293120).

Tuloeroja koskevat tilastot ja niistä lasketut tilastosuureet saavat aika-ajoin huomiota mediassa, tutkijoiden ja poliitikkojen puheenvuoroissa. Tuloerojen mittareita käytetään usein kahteen tarkoitukseen: ovatko tuloerot kasvaneet vai kaventuneet, tai ovatko tuloerot suuret vai pienet? Ylivoimaisesti suosituin käytetyistä tuloeromitoista on suhteellinen Gini-kerroin.1 Se saa arvoja nollan ja sadan välillä; nolla tarkoittaa, ettei tuloeroja ole lainkaan, ja 100 taas tarkoittaa tulojen keskittyneen yhdelle henkilölle. Valitettavan usein Gini-kertoimeen tutustuminen jää tähän tietoon. Varsin yleinen käsitys tuntuu olevan, että muutokset tuloeroissa ovat yhtä kuin muutokset Gini-kertoimessa.
Taustaksi tuloerojen mittaamiselle ja käytetyille mitoille on hyvä tarkastella, miten käytettävissä olevat tulot2 ovat kehittyneet eri kohdissa tulonjakaumaa. Kuviot 1 ja 2 esittävät reaalisten käytettävissä olevien tulojen kehityksen neljässä tulonsaajaryhmässä. Kussakin ryhmässä seurataan sekä ryhmän keskiarvoa että mediaania. Suurituloisin 20 prosenttia jaetaan kahteen ryhmään: suurituloisin prosentti ja loput tulonsaajat, kun ylin prosentti on siitä vähennetty (so. prosenttipisteiden 99 ja 80 väli). Seuraavaa ryhmä koostuu 60 prosentista tulojakauman keskeltä, jolloin pienituloisiksi jää 20 prosenttia. Useissa tutkimuksissa juuri tätä keskellä olevaa 60 prosenttia kutsutaan ”keskiluokaksi” (ks. esimerkiksi Atkinson ja Brandolini 2013).
Kuviosta 1 havaitaan, että tulokehitys on ollut varsin maltillista ”keskiluokassa” ja alimmassa 20 prosentissa. Keskimääräinen kasvu ylimmän 20 prosentin keskuudessa oli myös melko vaatimatonta verrattuna ylimpään yhteen prosenttiin, joka repäisi 1990-luvun jälkimmäisellä puoliskolla kaulaa muihin.
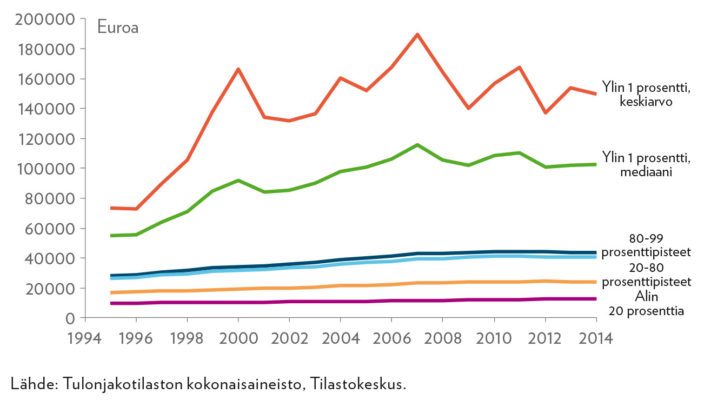
Jos mennään vielä ylemmäs ylimpään promilleen, kasvu on ollut aivan omissa lukemissaan3. Sen voi päätellä jo siitä, että kuviossa ylimmän yhden prosentin keskiarvo ja mediaani ovat loitonneet kauas toisistaan. Toisin kuin keskiarvoon, mediaaniin ei vaikuta kaikkein suurituloisimpien tulojen kasvu.4 Itse asiassa mediaanin ja keskiarvon suhde on kelpo tuloeromitta. Alimmassa ryhmässä mediaani ja keskiarvo ovat lähes samat kuvion skaalassa.
Kuvio 2 taas kuvaa suhteellista kasvua näissä samoissa ryhmissä. Ylimmän yhden prosentin tulot kasvoivat vuodesta 1995 vuoteen 2007 158 prosenttia, ”keskiluokan” 36 prosenttia ja alimman 20 prosentin 15 prosenttia. Kuvion 2 skaalan ei mahdu ylimmän promillen tulojen kasvua. Se oli tuolla ajanjaksolla 252 prosenttia!

Tuloeromitat ja tulonjakoarvostukset
Voidaanko tuloeromittojen avulla sanoa riidattomasti, miten voimakkaasti tuloerot kasvavat tai supistuvat? Jotta voimme vastata tähän, tarvitaan tietoa tuloeromittojen ominaisuuksista. Varsin yleinen harhakäsitys on, että Gini-kertoimeen ei sisälly tulonjakoarvotuksia, joten sitä kutsutaan usein tilastolliseksi tulonjakomitaksi. Gini-kerroin ei kuitenkaan ole puhtaasti tilastollinen mitta, vaan sen taustalla on implisiittisiä tulonjakoarvostuksia.
Gini-kerroin on erityisen herkkä tyypillisen tulonjakauman keskivaiheilla tapahtuville muutoksille. Se johtuu tulonjakoa koskevista arvostuksista: lisäeuro henkilölle, jonka tulot ovat suuremmat kuin 20 prosentilla pienituloisimmasta väestöstä, saa nelinkertaisen painon verrattuna henkilöön, jonka tulot ovat pienemmät kuin 20 prosentilla suurituloisimmasta väestöstä. Mitä suurempiin tuloihin mennään sitä pienemmän painon tulonlisäykset Gini-kertoimessa saavat5.
Gini-kerroin ei ole pelkkä tilastollinen tuloeromittari, vaan sen taustalla on lukkoon lyödyt tulonjakoa koskevat arvostukset.
Politiikkamuutosten tulonjakovaikutusten selvittäminen on yleistynyt myös Suomessa, mutta vaikutukset esitetään jostain syystä lähes aina suhteellisen Gini-kertoimen muutoksina. On syytä ihmetellä, miksi suhteellinen Gini-kerroin on niin hallitsevassa asemassa tuloeroja arvioitaessa. Ei ole ollenkaan selvää, mitä suhteellisen Gini-kertoimen muutos itse asiassa tarkoittaa.
Gini-kertoimen pieneneminen ei välttämättä tarkoita kaikkien mielestä eriarvoisuuden vähentymistä. Tiukasti ottaen se tarkoittaa sitä vain niiden mielestä, jotka hyväksyvät Gini-kertoimen taustalla olevat tulonjakoarvostukset. Näin ollen on tarpeellista tarkastella mittoja, jotka perustuvat eksplisiittisesti tulonjakoarvostuksiin. Tällöin puhutaan normatiivisista tulonjakomitoista.
Atkinsonin tuloeromitta ottaa huomioon eksplisiittisesti tulonjakoa koskevat arvostukset.
Klassikkoartikkelissaan Atkinson (1970) totesi, että kysymys tuloerojen muutoksista vaati arvoarvostelmien täsmentämistä. Hän myös kehitti mitan, joka tunnetaan Atkinsonin tuloeromittana. Atkinsonin mitta ottaa huomioon tulonjakotavoitteet niitä kuvaavan parametrin ε avulla. Tämä parametri kuvaa, miten paljon yhteiskunta panee painoa tuloerojen tasoittamiselle. Parametri ε saa arvoja nollasta äärettömään. Parametrin arvolla nolla yhteiskunta liittää saman hyvinvointipainon jokaiselle tulonsaajalle, ja arvolla ääretön yhteiskunta on kiinnostunut vain pienituloisimmasta tulonsaajaryhmästä.
Atkinsonin mitta ilmaisee sen osuuden nykyisistä kokonaistuloista, jotka tarvittaisiin nykyisen tulonjaon tuottaman hyvinvoinnin saavuttamiseksi tilanteessa, jossa tulot olisi jaettu tasan. Esimerkiksi jos Atkinsonin mitta saa arvon 0,15, niin nykyinen hyvinvointi voitaisiin saavuttaa jo 85 prosentilla nykyisistä kokonaistuloista6 (0,85 = 1–0,15). Vaihtoehtoinen tulkinta on, että uudelleenjaon avulla saatu tasaisempi tulonjako merkitsisi samaa kuin kokonaistulojen nostaminen 15 prosentilla. Näin ollen Atkinsonin mitta voidaan tulkita sekä eriarvoisuusmittana että indeksinä, joka ilmaisee tulojen uudelleenjaosta saatavan potentiaalisen hyvinvointivoiton.
Ovatko tuloerot suhteellisia vai absoluuttisia?
Suhteellisen näkemyksen mukaan tuloerot eivät muutu, vaikka kaikkien tulonsaajien tulot esimerkiksi kaksinkertaistuisivat. Kuvitellaan tilanne, jossa yhden tulot ovat 1000 euroa ja toisen tulot ovat 10000 euroa. Jos kummankin tulot jostain syystä kaksinkertaistuisivat, niin tulojen suhde pysyisi samana eli kymmenkertaisena. Sen sijaan absoluuttinen ero heidän tulojensa välillä muuttuu 9000 eurosta 18000 euroon. Olemmeko edelleen sitä mieltä, että tuloerot ovat pysyneet muuttumattomina?
PALKKOJEN PROSENTTIMÄÄRÄISET KOROTUKSET LISÄÄVÄT ABSOLUUTTISIA TULOEROJA.
Ranskalainen taloustieteilijä Serge Kolm (1976) havainnollisti asiaa esimerkillä Ranskasta. Vuoden 1968 toukokuun suurten mielenosoitusten seurauksena syntyi sopimus, jolla kaikkien palkkoja korotettiin 13 prosenttia. Kuitenkin monet mielenosoittajista kokivat tulleensa petetyiksi, koska yhtä suuri prosenttikorotus johti heidän mielestään eriarvoisuuden kasvuun. Kolm kutsui suhteellisia tuloeromittoja oikeistolaisiksi ja absoluuttisia mittoja vasemmistolaisiksi mitoiksi.
Sama asetelma on tullut esille monesti Suomessa, kun on kiistelty verojen tai palkkojen alentamisesta tai korottamisesta joko prosentti- tai euromääräisesti: oikeistolaiset ovat perinteisesti vannoneet prosenttimuutosten ja vasemmistolaiset euromääräisten muutosten nimeen. Vuoden 2018 palkkaneuvotteluissa Suomessa ajettiin kautta linjan ja suuremmitta soraäänittä läpi epäsolidaariset 3,2 prosentin korotukset.
Muita tuloeromittoja: logaritminen keskiarvopoikkeama ja tulo-osuudet
On toki muitakin tuloeromittoja kuin Gini-kerroin. Monet niistä toteuttavat samat ominaisuudet kuin suhteellinen Gini-kerroin. Esimerkki logaritminen keskiarvopoikkeama (MLD) toteuttaa samat ominaisuudet kuin suhteellinen Gini-kerroin, mutta sillä on muita ominaisuuksia, joiden takia monet tuloerotutkijat suosittelevat käytettäväksi sitä Gini-kertoimen sijasta7. Esimerkiksi MLD-mitta antaa saman painon tulon muutokselle kaikissa tulonjakauman kohdissa8. Atkinsonin mitan erikoistapauksessa ε=1 tuloerot muuttuvat Suomen tulonjakoaineistolla lähes identtisesti MLD-mitan kanssa.9
Tulonjakauman yhteen lukuun puristavat mitat eivät tietenkään pysty ottamaan huomioon kaikkia tuloeroihin vaikuttavia seikkoja. Näiden heikkouksien vuoksi suosituiksi ovat tulleet tulo-osuusmitat. Erityisesti näin on tapahtunut ylimpien tulo-osuuksien kehitystä arvioitaessa. Tulo-osuusmitat, jotka osoittavat suurituloisimman (varakkaimman) kymmenyksen tai prosentin osuuden kokonaistuloista (kokonaisvarallisuudesta), antavat selvästi konkreettisemman kuvan tuloeroista kuin abstrakti Gini-kerroin.
Tuloerojen kehitys Suomessa eri mittareiden mukaan
Kuviossa 3 verrataan suhteellista ja absoluuttista Gini-kerrointa10 ja logaritmista keskiarvopoikkeamaa (MLD). Siitä havaitaan, että mitat eroavat tuloerojen kasvun suhteen melkoisesti toisistaan. Suhteellinen Gini-kerroin kasvaa selvästi vähemmän kuin muut mittarit verrattaessa tuloerojen kehitystä aikavälillä 1990–2016 näillä kolmella mitalla.
Mikä selittää näitä eroja? Mitat eroavat toisistaan siinä, miten ne painottavat muutoksia eri kohdissa tulonjakaumaa ja miten ne reagoivat tulon muutoksiin keskiarvon yläpuolella11. Cowell ja Flachaire (2018) testasivat, miten tulonjakomitat reagoivat yhden henkilön tulon kasvuun keskiarvotulon yläpuolella. Tuntuisi luontevalta, että tuloeromitat kertoisivat tuloerojen kasvavan. Näin onkin MLD-mitan tapauksessa, mutta suhteellinen Gini-kertoimen mukaan tuloerot kaventuvat. Näiden kahden seikan vuoksi MLD-mitta reagoi voimakkaammin ylimpien tulojen kasvuun ja laskuun kuin suhteellinen Gini-kerroin.
MLD-mitta reagoi voimakkaammin ylimpien tulojen kasvuun ja laskuun kuin suhteellinen Gini-kerroin.
Kuvio 3 vahvistaa tämän Suomen aineistolla. Erityisesti MLD-mitta on reagoinut suhteellista Gini-kerrointa selvästi voimakkaammin ylimpien tulojen kasvuun sekä 1990-luvun jälkimmäisellä puoliskolla että ajanjaksolla ennen vuotta 2007. Esimerkiksi kun Suomessa 1990-luvun lopulla suurituloisimpien tulonsaajien käytettävissä olevien tulojen tulo-osuudet moninkertaistuivat12, Gini-kertoimen muutos oli huomattavasti maltillisempi.
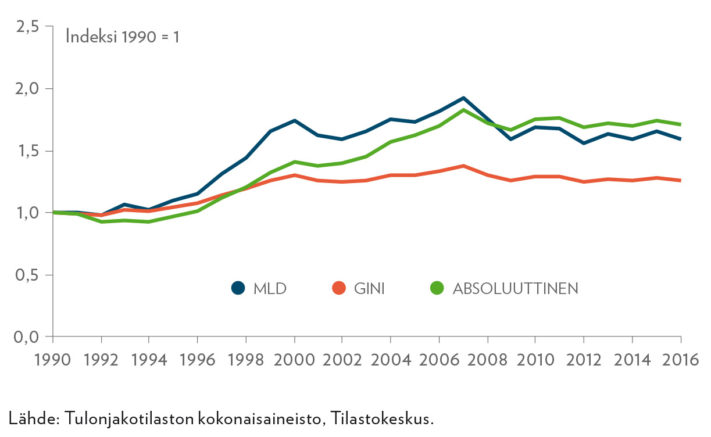
Kuviosta 3 nähdään niin ikään, että tuloerojen kasvu on ollut myös absoluuttisella Gini-kertoimella mitattuna hyvin yhtäjaksoista 1990-luvun puolivälistä aina vuoteen 2007. Absoluuttisella Gini-kertoimella mitattuna, kun myyntivoitot otetaan pois, kasvu on ollut yhtäjaksoista koko kuvion 3 kuvaaman periodin ajan.
Kuten kuviosta 1 huomattiin, ylimmän tulonsaajaprosentin reaalisten käytettävissä olevien tulojen mediaani ja keskiarvo loittonivat toisistaan. Tämä vihjasi siitä, että ylin promille tulonsaajista on erkaantunut kauas muun ylimmän yhden prosentin yläpuolelle. Tulo-osuudet ovat vaihtoehtoinen tapa kuvata ylimpien tulojen merkitystä tulonjakaumassa.

Kuviossa 4, joka perustuu vuodesta 1995 lähtien saatavissa olevaan tulonjaon kokonaisaineistoon, kuvataan ylimpien tulo-osuuksien kehitystä. Kaikkein suurituloisimman promillen bruttotulo-osuus oli vuonna 2000 lähes 40-kertainen heidän suhteelliseen väestöosuuteensa nähden. Vuonna 2007 se oli hiukan alle 30-kertainen ja viimeisinä vuosina noin 20-kertainen. Vuonna 1985 vastaava luku oli 5-kertainen (Riihelä ym. 2010). Vuoden 2007 jälkeen ylimmät tulo-osuudet näyttäisivät pienentyneen. Tästä syystä tuloeromittojen mukaan tuloerojen kasvu olisi pysähtynyt. Onko näin todellisuudessa tapahtunut? Palataan tähän hetken päästä.
Suomessa tulonjakauman yläpäässä verotus on regressiivistä: keskimääräinen veroaste laskee tulojen kasvaessa.
Kuviosta 4 havaitaan myös, että tulonsaajien ylimmän promillen käytettävissä olevien tulojen tulo-osuus on lähes sama kuin bruttotulojen tulo-osuus. Kun vertaa ylimmän promillen tilannetta ylimmän prosentin siihen tulo-osuuteen, josta on poistettu suurituloisin promille (väli 99,0–99,9), havaitaan erojen olevan huomattavasti pienemmät promillen käytettävissä olevien tulojen ja bruttotulojen tulo-osuuksissa välillä. Tämä viittaa siihen, että ylimmän promillen keskimääräiset veroasteet (maksetut verot suhteessa ansio- ja pääomatulojen kokonaissummaan) ovat pienemmät kuin välillä 99,0–99,9. Ylimmässä promillessa vuosina 2003 ja 2004 keskimääräiset veroasteet olivat jopa pienemmät kuin keskimääräinen veroaste keskimääräisen tulon kohdalla. Kuitenkin monet poliitikot toistelevat Suomen ennätyksellisen ankaraa progressiota.
Puuttuvat tulotiedot vaikeuttavat tulo- ja varallisuuserojen tutkimista
On kuitenkin perusteita epäillä, että kuvion 3 mittojen antamat arvot ja kuvioiden 4 ylimmän yhden prosentin ja varsinkin ylimmän promillen tulo-osuudet ovat alakanttiin. Erityisesti näin on vuoden 2005 veroreformin jälkeen. Osa ylimmistä tuloista on poissa tulonjakotilastoista. Tulonjakoaineistossa ei ole tietoa holding-yhtiöiden sisään jäävästä tulosta ja sen kehityksestä, joten emme tiedä, miten yrityksen tulo on kohdistunut sen omistajille.
Rahoitussektori on tarjonnut, eduskunnan hyväksymän lain ansiosta, veroilta suojautumista helpottamaan yrityksille ja varakkaille yksityishenkilöille erilaisia sopimuksia, niin sanottuja vakuutuskuoria13. Näiden sopimusten puitteissa kertyvät tulot (kuten osingot ja myyntivoitot) eivät näy tulonjakotilastoissa.14 Ne näkyvät vasta kun tuloja nostetaan näistä sopimuksista, mutta näin toteutunut varallisuuden kasvu ei näy varallisuustilastoissa. Sen sijaan niiden arvonnousuihin ei kohdistu tuloveroa.
Lisäksi varallisuusvero lakkautettiin vuonna 2005, ja veroparatiiseihin kätketyt tulot ja varallisuudet eivät tietenkään näy tilastoissa. Varallisuusaineistosta tiedämme varallisuuserojen kasvaneen pitkään jatkuneen taantuman aikanakin (ks. Riihelä ym. 2017, Törmälehto 2018). Kasvun moottorina on ollut listaamattomien osakeyhtiöiden nettovarallisuuden kasvu. Erityisesti rahoitusvarallisuus on kasvanut. Reaali-investoinnit taas olivat vahvasti laskutrendillä.
Vuoden 1993 veroreformi, jolloin ansiotulo- ja pääomatuloverotus eriytettiin, loi vahvan kannustimen osinkojen ja myyntivoittojen ottamiseen ulos yrityksestä. Vuoden 2005 reformi ja sen jälkeiset muutokset ovat jossain määrin kulkeneet eri suuntaan, mutta veroilta voidaan edelleen suojautua esimerkiksi sijoitus- tai holding-yhtiöiden avulla.
Varakkaiden henkilöiden käyttämien vakuutuskuorien sijoitustuotot eivät näy tulonjakotilastoissa.
Alstadsetter et al. (2016) arvioivat Norjan aineistolla, miten ylimmät tulo-osuudet muuttuvat, kun yrityksen sisään jäävä, veroilta suojassa oleva tulo otetaan huomioon. Norjan tilastokeskus pystyi rekisteritietojen avulla yhdistämään yrityksen tulon sen kaikille suorille ja epäsuorille omistajille. Tulokset olivat häkellyttäviä: esimerkiksi ylimmän tulonsaajapromillen tulo-osuuden havaittiin kaksinkertaistuneen Norjassa vuoden 2005 veroreformin jälkeen.15 Veroreformissa tehtiin suuri muutos ottamalla käyttöön osakkeenomistajan osinkovero, millä saatiin tulonmuunto kuriin, mutta samalla syntyi houkutus jättää tuloja yritykseen verolta suojaan.
Onko jotakin samanlaista tapahtunut Suomessa? Ei varmastikaan samassa määrin kuin Norjassa, sillä täällä voi Norjaan verrattuna ottaa listaamattomasta yrityksestä edelleen huomattavasti enemmän verovapaita osinkoja. Toisaalta pörssiosinkojen verotus on Suomessa kiristynyt, mistä johtuen varakkaille pörssiyhtiöiden omistajille tuli entistä suurempi kannustin suojautua veroilta holding-yhtiöiden avulla. Holding-yhtiön pörssiyhtiöstä saama osinko on verovapaata tuloa, jos se omistaa tämän osakepääomasta vähintään 10 prosenttia.
Pitemmän ajanjakson tulot ja tuloerot
Tähän asti tuloerojen tarkastelut perustuivat vuosittaiseen tulotietoon. Edellä esitetyt poikkileikkausjakaumat saattavat antaa niistä erilaisen kuvan kuin pitemmän ajan tulo. Useinhan väitetään, että tuloerojen kasvusta ei kannata välittää, koska tulot vaihtelevat vuosittain. ”Tänään on minun vuoroni, huomenna taas sinun.” Pitemmän aikavälin (eli pysyvämmän) tulon jakautuminen liittyy läheisesti liikkuvuuteen tulojakaumassa suurempiin tai pienempiin tuloihin päin. Miten tuloliikkuvuus vaikuttaa tuloeroihin, kun tarkastellaan pitemmän aikavälin tuloa?
Tulonjaon kokonaisaineiston avulla voimme seurata samojen ihmisten tulojen kehitystä pitemmällä ajalla. Henkilöiden tulot vaihtelevat enemmän tai vähemmän vuodesta toiseen. Näin ollen on selvää, että useamman vuoden keskitulot muuttuvat vähemmän kuin vuositulot ja että näin ne tasoittavat tuloeroja. Kuvio 5 osoittaa kuitenkin, että myös viiden vuoden keskituloilla laskettuna tuloerot ovat kasvaneet. Kasvu on ollut tasaista periodiin 2004–2008 asti. MLD-mitalla mitattuna ne ovat kasvaneet selvästi Ginillä mitattuja enemmän.
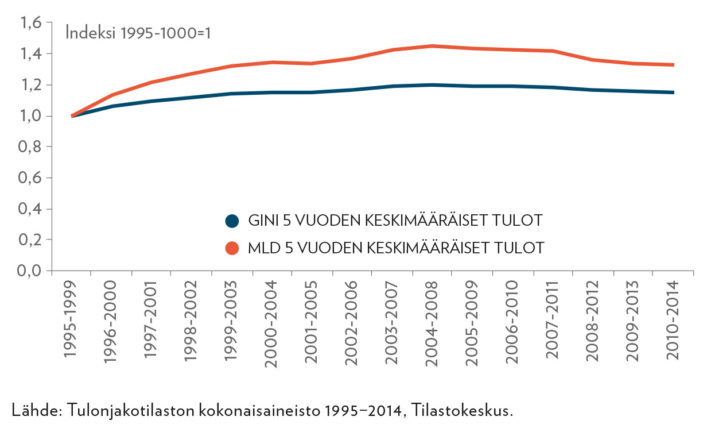
Useamman vuoden keskitulojen muuttumisella vuosituloja vähemmän on selvä yhteys siihen, kuinka henkilöiden tulot vaihtelevat vuodesta toiseen. Tätä muutosta tai toisinpäin tarkasteltuna pysyvyyttä voidaan mitata monella tavalla. Seuraava indikaattori kuvaa pysyvyyttä siten, että henkilö, joka tarkasteluperiodina ja sitä edeltävän kolmen vuoden aikana on ollut samassa tuloluokassa vähintään kaksi kertaa, kuuluu ns. pysyvään joukkoon.
Liikkuvuus ja pysyvyys eri tuloluokkien välillä vaikuttavat pitemmän aikavälin tulojen eroihin.
Tuloluokkien määrittely vaikuttaa siihen, kuinka pysyvästi henkilöt ovat tietyssä tuloluokassa. Jos luokituksen tekee tulokymmenyksittäin, pysyvyyttä on eniten ylimmässä ja alimmassa tulokymmenyksessä. Pysyvyys pienenee tasoltaan tulokymmenyksissä mediaanituloa kohti mentäessä ja kasvaa tulokymmenyksissä, jotka ovat mediaanitulon yläpuolella. Koska väestö keskittyy voimakkaammin keskitulon ympärille, ovat tulorajat keskimmäisissä tulokymmenyksissä lähempänä toisiaan kuin jakauman ääripäissä, joka helpottaa siirtymistä tuloluokasta toiseen. Pysyvyys keskimmäisissä tulokymmenyksissä on siksi pienempää.

PYSYVYYS ON KASVANUT ENITEN TULONSAAJIEN YLIMMÄSSÄ PROSENTISSA JA YLIMMÄSSÄ PROMILLESSA.
Kuviossa 6 tulokymmenyksiä on yhdistelty, ja pysyvyyttä tarkastellaan samoissa tuloryhmissä kuin kuvioissa 1 ja 2 eli alimmassa 20 prosentissa, ns. keskituloisilla (20–80 prosenttipisteissä), ylimmällä 20 prosentilla (pois lukien ylin prosentti), ylimmällä prosentilla ja ylimmässä promillessa. Keskituloisten (60 prosenttia väestöstä) kohdalla havaitaan, että pysyvyys on suurta. Olennaista on kuitenkin se, että pysyvyys on kasvanut ajassa kaikissa tuloryhmissä. Tarkasteltaessa tulonsaajien ylintä prosenttia ja promillea havaitaan, että pysyvyys on kasvanut eniten näissä tuloluokissa. Ylimmässä promillessa pysyvyys vaihtelee enemmän kuin ylimmässä prosentissa (kuvio 6).
Lopuksi
Suomalaisessa tuloerokeskustelussa tuodaan toistuvasti esille, että Suomen tuloerot ovat edelleen maailman pienimpiä ja että tuloerot eivät ole enää kasvaneet 2000-luvulla. Jälkimmäisen väitteen voi helposti kumota: tuloerot kasvoivat 1990-luvun puolivälistä vuoteen 2007 asti, ja pienen notkahduksen jälkeen ne ovat jääneet talouden taantuman aikana korkealle tasolle. Se, kuinka voimakkaasti tuloerot ovat sitten muuttuneet, on riippuvainen siitä, miten tuloeroja mitataan. Tuloeroja mitataan ja vertaillaan eri ajankohtien ja eri maiden välillä lähes aina suhteellisella Gini-kertoimella. Se asettaa pienen painon muutoksille ylimmissä tuloissa. Koska Suomessa suurimmat muutokset viimeisen reilun kahdenkymmenen vuoden aikana ovat tapahtuneet juuri ylimmissä tuloissa, Gini-kerroin, toisin kuin MLD-mitta, reagoi näihin muutoksiin lievästi.
Tulokehitystä arvioitiin vuositulojen lisäksi viiden vuoden keskiarvotuloihin perustuvilla mitoilla, jolloin voitiin ottaa paremmin huomioon voimakkaasti vaihtelevien tuloerien, kuten myyntivoittojen, vaikutus tuloeroihin. Näinkin arvioitu tuloerokehitys vahvistaa tuloerojen kasvaneen yhtäjaksoisesti 2000-luvun ensimmäisen vuosikymmenen loppupuolelle asti. Pysyvyys sekä ylimmissä että alimmissa tuloryhmissä on sitkistynyt viimeisten vuosikymmenten aikana. 1990-luvulta lähtien tuloerokehityksessä on ilmennyt vahvistuvaa polarisoitumista molempiin suuntiin mediaanitulosta. Ylimpien tuloryhmien kasvattaessa osuuttaan kokonaistuloista alimmat ja keskituloiset ryhmät ovat menettäneet osuuttaan.16
Tuloerojen kehitystä arvioitaessa on syytä muistaa, että verojärjestelmämme tarjoaa edelleen varakkaille omistajille verosuunnittelureitin. Se on mahdollistanut 1990-luvun puolivälin jälkeisen roiman tuloerojen kasvun. Näin ollen mitään esteitä ei ole ylimpien tulo-osuuksien kasvulle jatkossakaan.17 Lisäksi vakuutuskuorissa ja holdingyhtiössä veroilta suojassa olevien tulojen puuttumisen vuoksi tuloeromitoilla mitatut tuloerot ja ylimmät tulo-osuudet ovat artikkelimme kuvioissa aliarvioita. Erityisesti tämä koskee tuloerokehitystä viimeisen kymmenen vuoden ajalta.
Aineistopuutteista huolimatta voimme sanoa, että tuloerot ovat Suomessa kasvaneet voimakkaammin kuin on luultu suhteellisen Gini-kertoimen perusteella. Väitteet Suomen pienistä tuloeroista moniin muihin maihin verrattuna perustuvat myös Gini-kertoimiin. Gini-kertoimilla mitatut tuloerot ovat kasvaneet reippaasti myös maissa, joita on totuttu pitämään pienten tuloerojen maina, kuten Pohjoismaissa (Aaberge et al. 2018).
Kirjoittajat
Marja Riihelä
erikoistutkija
VATT
marja.riihela at vatt.fi
Matti Tuomala
tutkimusjohtaja, professori emeritus
TAMPEREEN YLIOPISTO
matti.tuomala at tuni.fi
Viitteet
1 Gini-kertoimessa kaikkien tuloparien vertailut suhteutetaan keskimääräiseen tuloon. Gini-kerroin on saanut nimensä italialaiselta tilastotieteilijältä Corrado Giniltä (1912). Hänen ansionsa oli lähinnä mitan popularisoinnissa.
2 Käytettävissä olevat tulot saadaan, kun kotitalouden palkka-, yrittäjä- ja pääomatuloihin lisätään saadut tulonsiirrot ja vähennetään maksetut välittömät verot. Ekvivalenttitulo on tulokäsite, jolla pyritään saamaan erityyppisissä kotitalouksissa asuvat henkilöt vertailukelpoisiksi. Tämä saadaan jakamalla kotitalouden tulot kulutusyksikköluvulla. Artikkelissa kulutusyksikkönä käytetään kulutusyksikkölukua, jossa kotitalouden ensimmäinen aikuinen saa painon 1, seuraavat yli 13-vuotiaat painon 0,5 ja lapset painon 0,3. Analyysissä tarkastellaan siis henkilöitä, joiden saamiin ekvivalenttituloihin vaikuttaa sen kotitalouden kokonaistulot, jossa henkilö asuu. Riihelä ym. (2010) osoittavat, että ylimmät tulo-osuudet ovat suuremmat yksilötuloilla kuin ns. ekvivalenttituloilla, joissa on otettu huomioon kotitalouden mittakaavaedut. Tulos ei ole yllättävä, koska ylimpiä tuloja on ennen muuta vanhemmilla kotitalouksilla, joissa ei ole enää lapsia.
3 Suurituloisimpaan promilleen kuuluu Suomessa noin 5 000 henkeä. Ylimmän promillen tulot olivat keskimäärin 143 000 euroa vuonna 1995, 445 000 euroa vuonna 2007 ja 318 000 euroa vuonna 2014.
4 Mediaani on tulojen suuruuden mukaan järjestetyn tulonjakauman keskimmäinen havainto.
5 Jos tulojakauma esitetään diskreettinä jakaumana, Gini-kertoimen tulonjakopainot voidaan esittää kaavana [2–(2i–1)/n] (*), missä i viittaa tulonsaajan järjestyslukuun tulonjakaumassa ja n on tulonsaajien lukumäärä. Köyhimmälle i=1, jolloin paino lähestyy kakkosta, kun n tulee suureksi. Rikkaimmalle henkilölle se on 1/n, joka taas lähestyy nollaa, kun n tulee suureksi. Mediaanitulonsaajalle (*) on 1, jos n on pariton luku.
6 Atkinsonin mitta parametriarvolla ε = 1 sai arvon 0,153 Suomessa vuonna 2016.
7 Esimerkiksi näin tekevät London School of Economicsin professori Frank Cowell ja ranskalaisekonomisti Emmanuel Flachaire (2018).
8 MLD = log (m/g) = log(m)–log(g), missä m on aritmeettinen ja g on geometrinen keskiarvo. Toisin ilmaistuna se on logaritminen ero aritmeettisen ja geometrisen keskiarvon välillä. On selvää, että laskettaessa näitä kahta keskiarvoa jokainen tulo saa saman painon.
9 Atkinson mitassa (A), parametriarvolla ε = 1 nykyisen tulonjaon tuottama hyvinvointi, kun tulot olisivat jaettu tasan, vastaa geometrista keskiarvoa eli A=1–g/m.
10 Absoluuttinen Gini-kerroin saadaan kertomalla suhteellinen Gini-kerroin keskimääräisellä tulolla.
11 He kutsuivat tätä ominaisuutta englanniksi käsitteellä ”monotonicity in distance”.
12 Entinen kansanedustaja Osmo Soininvaara kirjoitti blogissaan 27.12.2018: ”Viime vuosina peliyhtiö Supercellin ilmiömäinen menestys on lisännyt Suomessa tuloeroja. Ilman sitä Gini-kerroin olisi nyt pienempi”. On totta, että huipputulojen kasvu on lisännyt tuloeroja. Mutta muutaman pelialan suurituloisen vaikutus suhteelliseen Gini-kertoimeen on kuitenkin lähes olematon (ks. alaviite 5).
13 Tyypillisimpiä vakuutuskuoria ovat kapitalisaatiosopimus (tai varainhoitosopimus), sijoitusvakuutus ja säästövakuutus.
14 Ei ole olemassa edes tarkkoja arviota näissä sopimuksissa olevien tulojen ja varojen kokonaissummasta. VM:n arvioiden mukaan varojen kokonaissumma on noin 40 miljardia. Riihelä ja Tuomala (2018) arvioivat, kuinka näiden varojen tuottojen huomioon ottaminen vaikuttaisi eri tulotasoilla bruttotulojen tulo-osuuksiin. Arviossa oletettiin, että vakuutuskuoriin ovat sijoittaneet bruttotulojen ylimpään desiiliin kuuluvat. Tuotoksi pääomalle on arvioitu joko 3 tai 5 prosenttia. Lisäksi tuottojen jakauma perustuu osinkotulojen jakaumaan: Ylimmän desiilin alin 9 prosenttia saa 37 prosenttia, ylin yksi prosentti saa 63 prosenttia. Ylin promille saa 35 prosenttia ja promillen ylin kymmenys 17 prosenttia tuotoista. Ylimmän yhden prosentin bruttotulo-osuus kasvoi lähes yhdellä prosenttiyksiköllä vuonna 2014. Ylimmän promillen ylimmän kymmenyksen tulo-osuus kasvoi 26 prosenttia. Lisäksi tarvittaisiin tietoa holdingyhtiössä olevista varoista ja niiden tuotoista.
15 Samalla menetelmällä arvioitiin myös vuotta 2005 edeltävät vuodet. Osuudet eivät juurikaan muuttuneet. Näin ollen veroreformeilla voi olla yllättäviä sivuvaikutuksia.
16 Ks. Riihelä ja Tuomala (2019).
17 Tulonjaon kokonaisaineisto (joulukuu 2018) viittaa myös tähän suuntaan. Voimakkaimmin oli vuonna 2017 kasvanut ylimmän 5 prosentin tulot. Valitettavasti tätä ylimpien tulojen kasvusta Tilastokeskus ei tiedotteessaan kerro. Aineisto ei ole myöskään tätä kirjoitettaessa Tilastokeskuksen ulkopuolisten tutkijoiden käytössä.
Kirjallisuus
Aaberge, R. & André, C. & Boschini, A. & Calmfors, L. & Gunnarsson, K. & Hermansen, M. & Langørgen, A. & Lindgren, P. & Orsetta, C. & Pareliussen, J. & Robling, P.-O. & Roine, J. & Søgaard, J. (2018), Increasing Income Inequality in the Nordics, Nordic Economic Policy Review 2018.
Alstadsæter, A. & Jacob, M. & Kopczuk, W. & Telle, K. (2016), Accounting for Business Income in Measuring Top Income Shares: Integrated Accrual Approach Using Individual and Firm Data from Norway, NBER Working Papers 22888.
Atkinson, A.B. (1970), On the Measurement of Inequality, Journal of Economic Theory, 2, 244–263.
Atkinson, A.B. & Brandolini, A. (2013), On the Identification of the Middle Class, teoksessa Gornick, J.C. & Jäntti, M. (Eds.): Income Inequality: Economic Disparities and the Middle Class in Affluent Countries, Stanford, CA: Stanford University Press, 77–100.
Cowell, F. & Flachaire, E. (2018), Inequality Measurement and the Rich: Why Inequality Increased More than We Thought, London School of Economics, STICERD, Public Economics Programme Discussion Paper.
Kolm, S.-C. (1976), Unequal Inequalities I, Journal of Economic Theory, 12, 416–442.
Riihelä, M. & Tuomala, M. (2018), Ylimmät tulo-osuudet, tuloerot ja verot, esitys 25.10.2018 Sosiaalipolitiikan päivillä, Tampereen yliopisto.
Riihelä, M. & Tuomala, M. (2019), Polarisaatiosta ja keskiluokan katoamisesta, ilmestyy Yhteiskuntapolitiikka-lehdessä.
Riihelä, M. & Sullström, R. & Tuomala, M. (2017), Varallisuus ja varallisuuserot Suomessa, Talous & Yhteiskunta 2/2017.
Riihelä, M. & Sullström, R. & Tuomala, M. (2010), Trends in Top Income Shares in Finland 1966–2007, VATT Rerearch Reports 157.
Törmälehto, V-M. (2018), Varallisuuserot kasvussa, tuloerot vakaat? Tieto & Trendi.


