Talouskasvu loppuu aikanaan, vai loppuuko?
Olemme tottuneet ajattelemaan, että talouskasvu jatkuu aina vain – onhan se jatkunut ennenkin. Tämä pitää kuitenkin paikkansa oikeastaan vain, jos katsomme 1900-luvun jälkimmäistä puoliskoa. Pidemmälle historiaan mentäessä talouskasvu on usein ollut olematonta. Tulevaisuudelle saadaan hyvin erilaisia kasvuennusteita riippuen siitä, oletetaanko tuottavuuden kasvun olevan vakiosuuruista vai oletetaanko kasvunopeuden olevan vakio.
Viimeisen 200–300 vuoden ajanjakso on tuudittanut meidät uskomaan, että huominen on aina parempi kuin tänään. Tulot ja kulutus kasvavat, lapsillamme on parempi elintaso kuin meillä. Koska näin on ollut jo monen sukupolven ajan, miksi tämä kehitys pysähtyisi? Miksi tosiaan, koska kaiken aikaa tietämyksemme kasvaa, kaiken aikaa tehdään uusia keksintöjä, ihmiset siirtyvät uusiin tehtäviin ja uusille (tuottavimmille) aloille ja niin edelleen.
Mutta vaikka näin onkin, voi olla, että meitä vaivaa jonkinlainen vauhtisokeus ja lyhytnäköisyys. Tarkastelemme historiaa vain muutaman vuosikymmenen ajanjaksolta ja unohdamme häveliäästi sadat ja tuhannet vuodet, jolloin talouskasvu on ollut lähestulkoon olematonta. Taloudesta puhuttaessa kaikki kulminoituu kasvuun ja kaikki ilmaistaan kasvuprosentteina. Ajattelutapaamme on syvästi iskostunut tapa projisioida lähivuosikymmenten kasvuprosentteja kauas tulevaisuuteen ikään kuin talouskasvun perusilme noudattaisi samaa kaavaa.
Ranskalainen taloustieteilijä Thomas Philippon julkaisi kaksi vuotta sitten mielenkiintoisen tutkimuksen1 tuottavuuden kasvun perusluonteesta. Hän esitti siinä kaksi vaihtoehtoista tapaa formuloida kasvun perusolemus.
Ensimmäinen tapa on perinteinen eksponentiaalisen kasvun luonnehdinta, jossa tuottavuuden kasvunopeuden oletetaan oleva vakio. Toinen vaihtoehto on yksinkertaisesti olettaa, että absoluuttinen kasvu on vakio. On tietysti selvää, että ajan oloon tämä lineaarisen kasvun mallin tulema poikkeaa huomattavasti eksponentiaalisen kasvun mallin tuloksesta, koska jos vaikkapa muuttuja A kasvaa määrän 1, kasvuvauhti riippuu luonnollisesti A:n suuruudesta. A:n kasvaessa kasvuvauhti automaattisesti supistuu, jos absoluuttinen kasvu pysyy samana. Olkoon A vaikka palkka. Kyse on silloin samasta asiasta kuin nouseeko palkka yhdellä eurolla vaiko yhdellä prosentilla. Eli tarkasteltavan muuttujan aikasarjat ovat aivan erinäköisiä, mikä ilmenee oheisesta kuviosta 1.
Kuvio 1. Lineaarinen vs. eksponentiaalinen kasvu
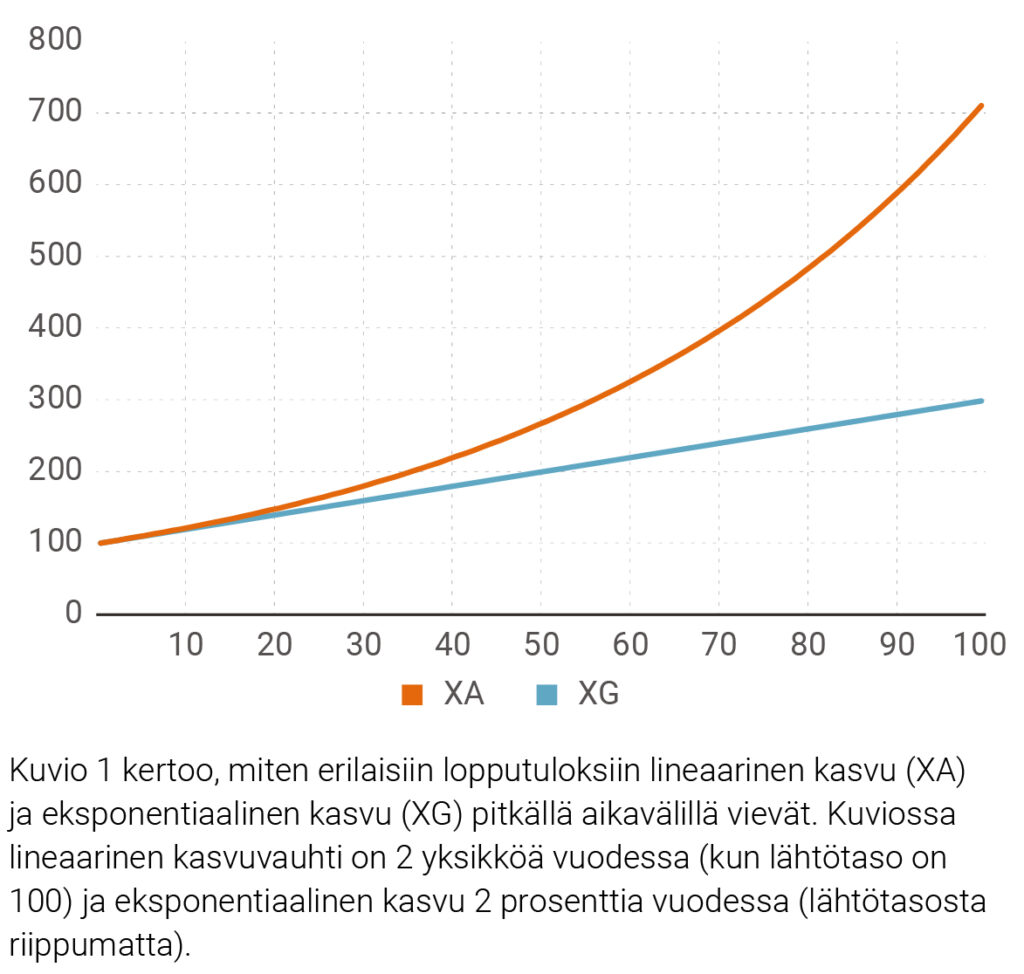
Philipponin tutkimuksessa on runsaasti näyttöä siitä, että lineaarisen kasvun malli on pitkällä aikavälillä huomattavasti parempi kuvaamaan ja ennen kaikkea ennustamaan niin kokonaistuottavuuden kuin kokonaistuotannon kasvua.
Kokonaistuottavuus A, jota usein kutsutaan tekniseksi kehitykseksi, on siinä mielessä hankala käsite, että sitä ei voi suoraan mitata, vaan se on ehdollinen paitsi tuotantofunktiolle, myös tuotantopanosten mittaamiselle2. Tyypillinen ongelma on se, mitataanko työllisyyttä nuppiluvulla, työtunneilla vaiko laatukorjatulla työpanoksella. Myös pääoman osalta voidaan tehdä laatukorjauksia esimerkiksi pääoman iän suhteen. Ongelma ei suinkaan ole mikään uusi, vaan siitä on keskusteltu pitkään3.
Tässä yhteydessä emme kuitenkaan paneudu mittaamisongelmiin paitsi pääoman iän suhteen, koska meillä ei ole mahdollisuuksia muuttaa käytettävissä olevien tilastojen luokituksia. Käytämme nimittäin ranskalaisten ekonomistien BCLD-tietokantaa (BCLD 2023), joka kattaa 23 läntistä teollisuusmaata ajanjaksolta 1890–2022. Tietokannassa muuttujat on muodostettu samalla tavalla, mikä mahdollistaa maakohtaiset vertailut.
Lineaarinen vai eksponentiaalinen kasvu?
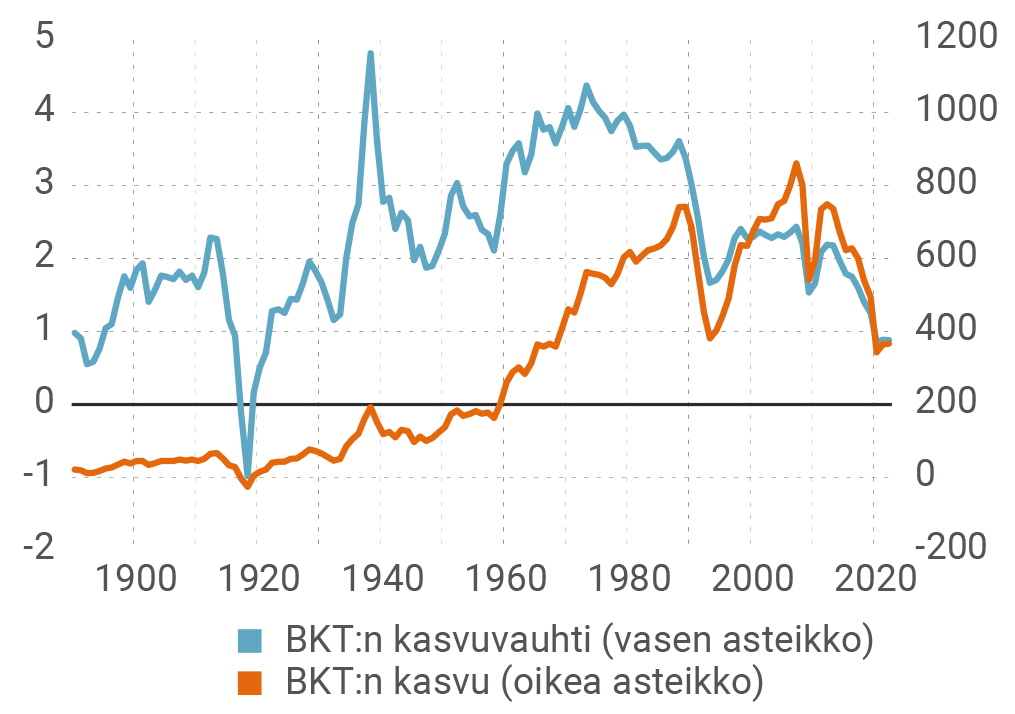
Muutama sana lienee paikallaan tuottavuuskehitystä koskevien lukujen perusluonteesta. Kuvio 2 kertoo, että BKT:n ja kokonaistuottavuuden kasvuvauhdit kulkevat ”käsi kädessä”. Tämä viittaa siihen, että BKT:n kasvun kannalta olennainen tieto on juuri kokonaistuottavuuden kehitys. Toisin sanoen, työpanokselle ja pääomalle jää vähemmän olennainen rooli. Toisaalta nähdään, että pääomaintensiivisyyden (pääoman ja työpanoksen suhteen) ja kokonaistuottavuuden (teknisen kehityksen) välillä on vissi riippuvuus, joka heijastaa yritysten pitkän aikavälin optimaalista pääomakantaa.
Kuvio 2. Kokonaistuottavuus, BKT:n kasvu ja pääomaintensiivisyys 23 maassa 1890–2022
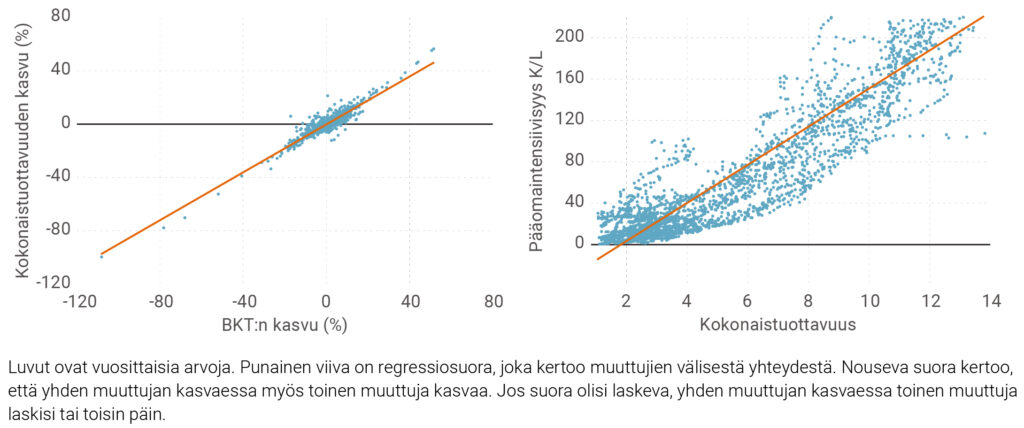
TALOUSKASVUN MITTAAMISESTA JA KÄSITTEISTÄ
Perinteisen eksponentiaalisen kasvun luonnehdinta on sellainen, jossa esimerkiksi kokonaistuottavuuden (jota usein tulkitaan ”tekniseksi kehitykseksi”) A osalta kirjoitetaan liikeyhtälö seuraavasti At = At-τ*(1+g)τ, jossa g on vakioinen kasvuvauhti. Eli ajatellaan, että taloudessa kaikki kasvaa g % ajanjakson τ (esimerkiksi vuoden) aikana. Lineaarisen kasvun ajatus taas on se, että tuottavuus A kasvaa tietyn vakiomäärän, esimerkiksi a:n verran. Tällöin formulointi on yksinkertaisesti seuraava: At = At-Τ + aτ.
Kokonaistuottavuus A ei tietenkään ole sama asia kuin kokonaistuotanto (BKT) tai työn tuottavuus. Kokonaistuotantoa mallitetaan monesti Cobb-Douglas-tuotantofunktiolla, joka on muotoa: Qt = AtKtαLt1-α, jossa α on pääoman K panosjousto L:n viitatessa työpanokseen. Työn tuottavuus Qt/Lt on tällöin yhtä kuin At(Kt/Lt)α, eli työn tuottavuus riippuu sekä kokonaistuottavuudesta (”teknisestä kehityksestä”) A että pääomaintensiivisyydestä K/L. Voiton maksimoinnin ensimmäisen kertaluvun ehdosta saadaan tällöin lause, joka liittää toisiinsa pääomaintensiivisyyden k =K/L ja pääoman vuokran reaalisin termein (vuokra-sanan sijaan puhumme usein käsitteestä user cost, jota merkitsemme tässä uc:lla) seuraavasti: (1-α)k = αA/uc. Jos uc on vakio, pääomaintensiivisuuden ja teknisen kehityksen välillä on lineaarinen riippuvuus. Näin itse asiassa näyttää olevankin kansainvälisessä datassa (kuvio 2).
Mitä sitten tulee kokonaistuottavuuden ja työn tuottavuuden kasvuun, se selviää kuviosta 3. Ilmenee, että ero näiden kahden käsitteen välillä on verraten pieni. Tämä viittaa siihen, että pääomapanoksen rooli on jatkuvasti pienentynyt 1970-luvun jälkeen. Tulos ei ole mitenkään yllättävä, kun tarkastelee nettoinvestointien kehitystä viimeisen 40 vuoden aikana. Se on ollut todella vaatimatonta lähes kaikissa maissa.
Kuvio 3. Kokonaistuottavuuden ja työn tuottavuuden kasvun vertailu 23 maassa vuosina 1890–2022
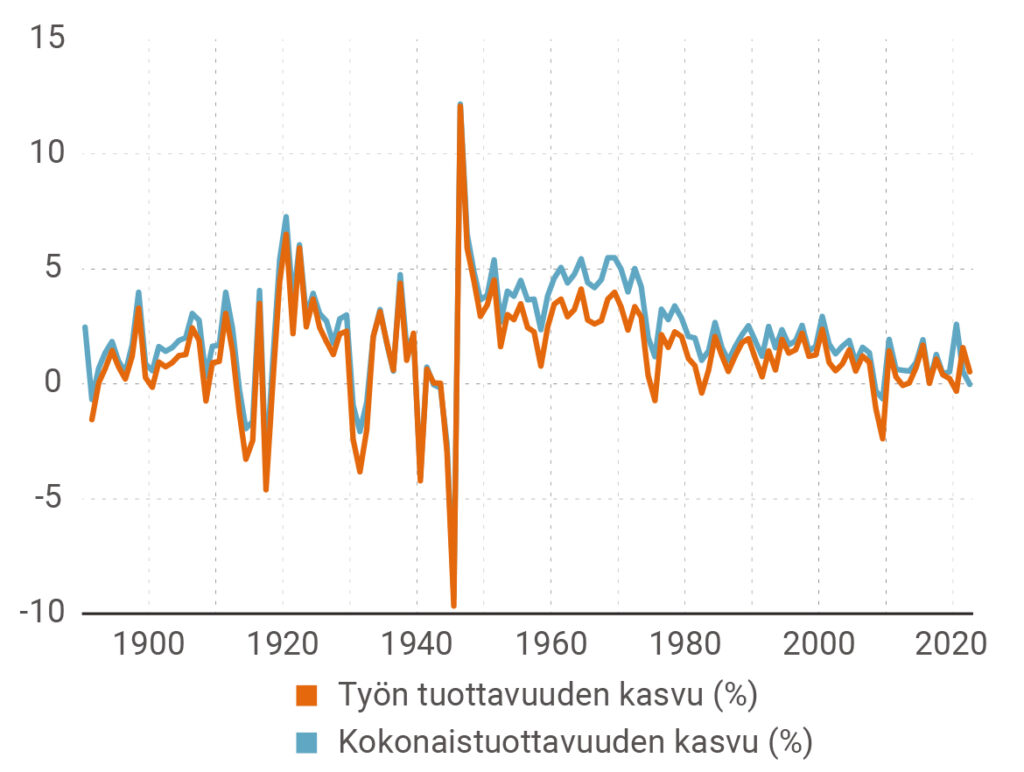
Maiden välillä on verraten pieniä eroja tuottavuuden trendin suhteen, mutta yksittäisten vuosien luvut poikkeavat toki paljon toisistaan. Erityisesti tämä koskee tietenkin ajanjaksoa 1890–1949. Niinpä koko ajanjaksolta 1890–2022 laskettujen maiden välisten korrelaatioiden keskiarvo on vain 0.13, eli luvut ovat hyvin erilaisia. Jos korrelaatio olisi 1, maiden tuottavuudet riippuisivat täysin toisistaan. Jos arvo olisi 0, maiden tuottavuuksilla ei olisi lainkaan yhteyttä.
Kun tarkastellaan ajanjaksoa 1950–2022, luku on jo 0.30 ja jos edetään 2000-luvulle (2000–2022), luku on 0.34, eli maittaiset luvut ovat entistä lähempänä toisiaan, vaikka täydellisestä samankaltaisuudesta ei voi puhua. Jos eri maiden luvuista lasketaan parhaan selitysvoiman omaava pääkomponentti, senkin kuvaaja antaa hyvin samanlaisen kuvan tilanteesta. BKT:n kasvulukujen osalta jonkinasteinen konvergenssi on paljon selvempää, mikä käynee ilmi seuraavista keskimääräisten korrelaatiokertoimien arvoista: 1891–2020: 0.19; 1950–2022: 0.43 ja 2000–2022: 0.684. Ilmeinen selitys tapahtuneelle on globalisaatio: taloudet ovat tulleet entistä riippuvaisemmiksi toisistaan kasvaneen ulkomaankaupan ja sijoitustoiminnan ansiosta.
Mitä sitten tulee Suomeen, havaitaan, että 2000-luvulla Suomi on selvästi alisuoriutuja, käytetään verrokkina sitten kaikkia muita 22 teollisuusmaata tai muita Pohjoismaita (kuvio 4). Aina 2000-luvun alkuun asti Suomen kehityskulku oli vertaansa vailla, mutta sen jälkeen tuottavuuden (niin työn tuottavuuden kuin kokonaistuottavuudenkin osalta) kasvu on lähestulkoon pysähtynyt. Ensi alkuun selitykseksi kelpasi Nokia, mutta loputtomiin lohduttomia lukuja on vaikea sillä selittää.
Kuvio 4. Kokonaistuottavuuden kehitys Pohjoismaissa vuosina 1890–2022
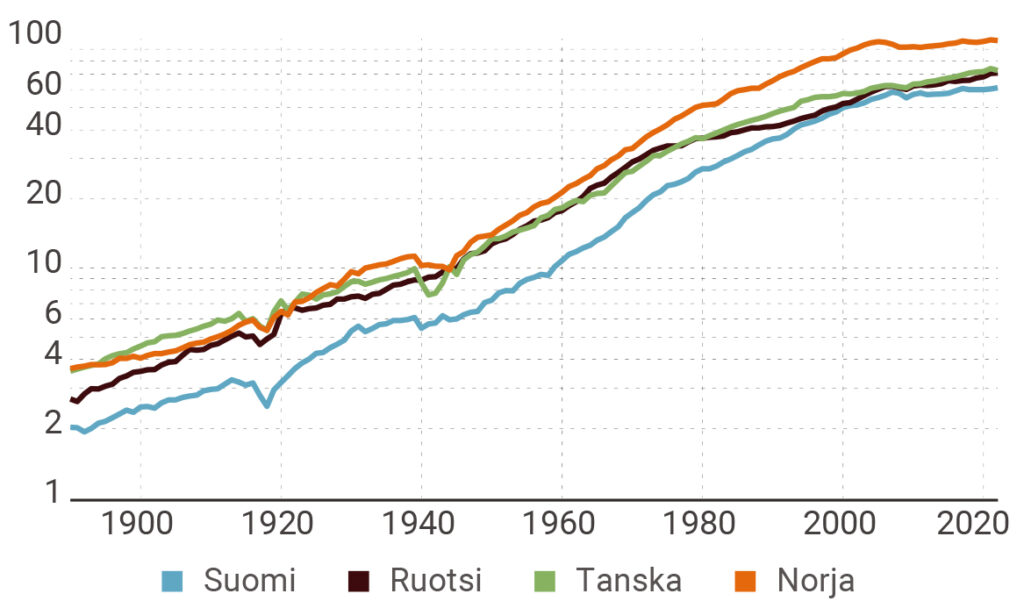
Muut selitykset, kuten rahoituksen saatavuus, työvoimapula, verotus, Venäjän sanktiot ja niin edelleen, eivät ole olleet kovin vakuuttavia, vaikka niissä kaikissa hiven totuutta olisikin. On myös epäilty, että erilaiset mittaustekniset ongelmat ovat syynä toteutuneeseen kehitykseen, mutta siltäkään osin ei ole saatu paljoa näyttöä, jos kohta selityksenä se on kaikkien hankalin.
Ennusteita tuleville vuosille
Philipponin analyysin kannalta olennainen kysymys on, miten kilpailevat kasvuhypoteesit kykenevät ennakoimaan talouskasvua. Missä määrin ja miten toteutunut kasvu projisoituu tulevaan kehitykseen? Kysymys on aiheellinen, koska tiedämme, että kokonaistuottavuuden arvot peräkkäisinä vuosina ovat hyvin voimakkaasti riippuvaisia toisistaan eli (auto)korreloituneita (paneeliaineistossamme ensimmäisen asteen autokorrelaatiokerroin on 0.98). Kokonaistuottavuuden kasvu sen sijaan on vain heikosti autokorreloitunut. Kasvuvauhdin autokorrelaatiokerroin on 0.10 ja kasvunkin vain 0.21).
Missä määrin ja miten toteutunut kasvu projisoituu tulevaan kehitykseen?
Kokonaistuotannon eli BKT:n kasvunumerot saattavat silti olla hyvin samanlaisia vuodesta toiseen, mutta jos aikahorisonttia pidennetään, ei enää ole helppoa sanoa, mikä on ”normaali” kasvuvauhti. Katsotaan vaikka Suomen BKT:n kasvua vuosina 1861–2022. Jos lasketaan kasvunumeroista 20 vuoden liukuva keskiarvo, saadaan jonkinlainen käsitys siitä, millaisia ajanjaksoja aiempina vuosikymmeninä on ollut. Selvästikin voidaan löytää ajanjaksoja, jolloin kasvuvauhti on ollut vain prosentin luokkaa, muutamaan otteeseen kasvuvauhti on pysytellyt kahden prosentin lukemissa, mutta selvän poikkeuksen muodostaa ajanjakso 1960–1990, jolloin keskimääräinen (henkeä kohden laskettu) kasvu lähenteli neljää prosenttia. Aivan viime vuosina on romahdettu yhden prosentin pintaan.
Selvästikin on mahdollista saada mitä tahansa kasvulukuja projisoitaessa historiallisen kehityksen valossa tulevaisuutta, kun vain valitaan sopiva vertailuajanjakso. Suomen luvut eivät kovin paljon poikkea yleisestä tendenssistä, mutta toki on syytä huomata, että keskimääräinen kasvuvauhti 2000-luvulla on vain kolmannes koko 1890–2022 ajanjakson arvosta.
Mieleen tulee silloin väistämättä kysyä, miten projisoinnit pitäisi tehdä. Pitäisikö olettaa kasvuvauhtien vaiko tuotannon (tai tuottavuuden) tason muutosten pysyvän kutakuinkin vakioina? Jonkinlaisen käsityksen tilanteesta saamme, jos vertaamme kasvuvauhdin ja kasvun liukuvien keskiarvojen aikasarjoja (kuvio 5)5. Selvästikin ero on siinä, että kasvunopeuden sarjassa on enemmän äärimmäisiä havaintoja verrattuna lineaarisen kasvun mallin mukaisen esitykseen.
Kuvio 5. Kokonaistuottavuuden kasvun 20 vuoden liukuva keskiarvo Suomelle 1890–2022
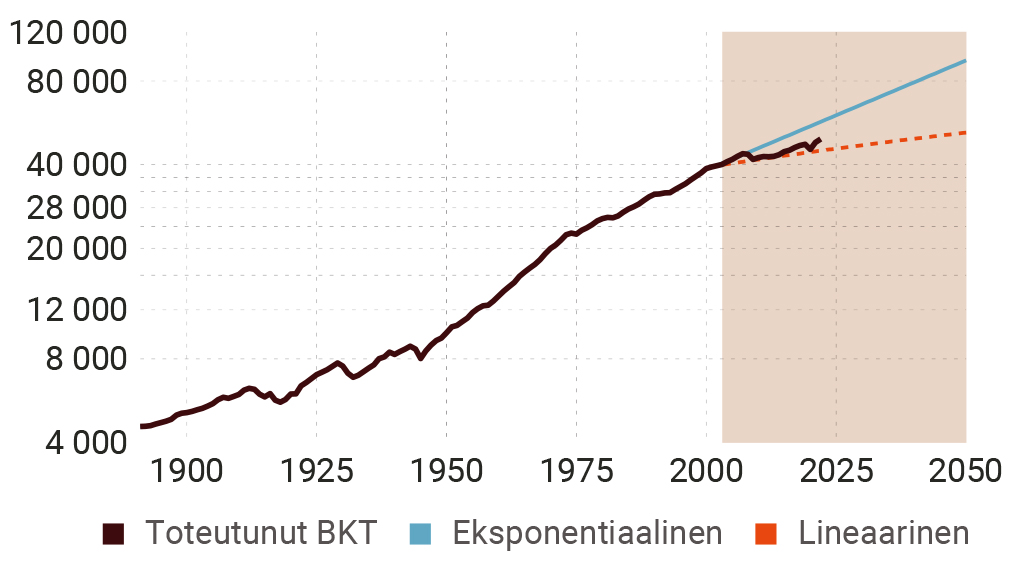
Mutta ex ante -ennusteissa, niin koko paneeliaineistolle kuin Suomelle, ero on silmiinpistävän suuri, ainakin jos tarkastellaan 2000-lukua (tarkemmin sanoen viimeistä 20 vuotta). Eksponentiaalisen kasvun malli ”ampuu selvästi yli”, kun taas lineaarisen kasvun malli vastaa aika hyvin tapahtunutta kehityskulkua (kuviot 6 ja 7).
Kuvio 6. BKT-ennuste 23 teollisuusmaalle vuosina 2023–2050 vuosien 1890–2002 datan perusteella
Kuvio 7. BKT:n ennuste Suomelle vuosien 1890–2002 datan perusteella
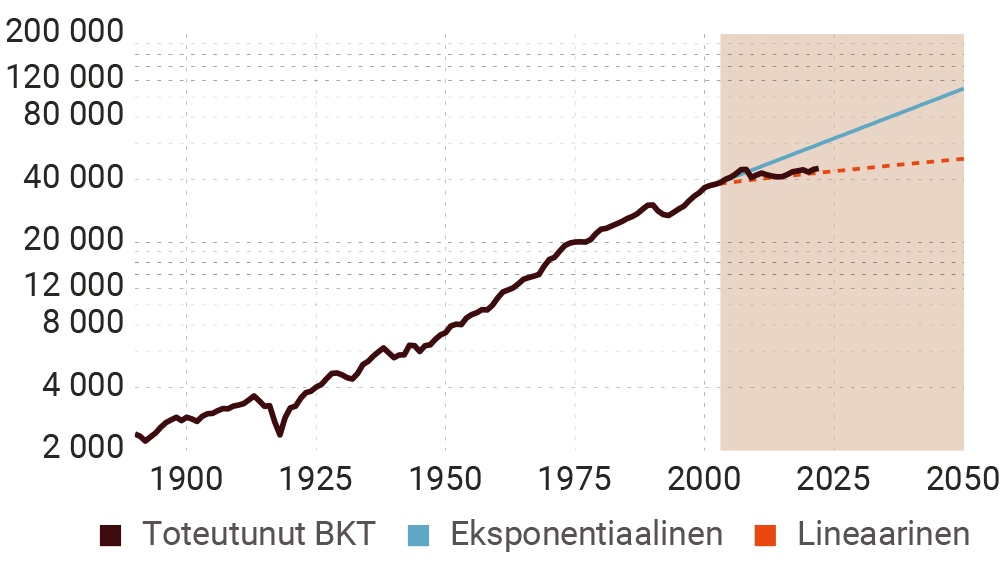
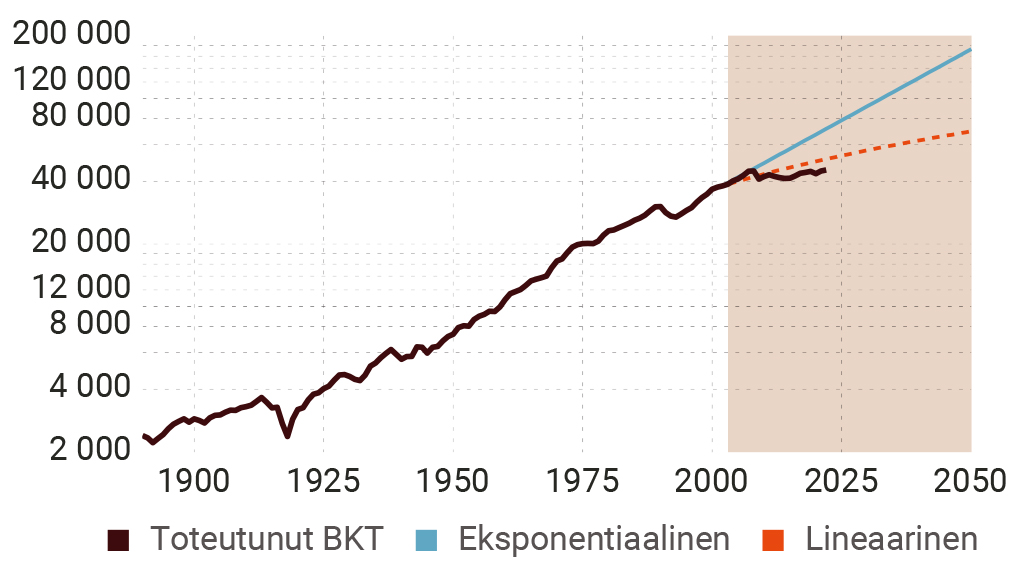
Ongelma on kuitenkin siinä, että ennustemallin otosajanjakson valinta vaikuttaa tuloksiin huomattavan paljon. Se näkyy selvästi, jos tarkastellaan Suomen tilannetta ja valitaan otokseen joko ajanjakso 1860–2002 tai 1950–2002 BKT:n osalta tai vastaavasti 1890–2002 ja 1950–2002 kokonaistuottavuuden osalta (kuviot 8–9). Selvää on se, että eksponentiaalisen kasvun malli ampuu aina yli ainakin 2000-luvun alun datan osalta, ja 2023–2050 ajanjaksokin näyttää epäilyttävältä. Lineaarisen mallin osalta otosajanjakso on erityisen kriittinen kokonaistuottavuuden suhteen. Jos valitaan ajanjakso 1950–2002, ennuste ampuu yli jo 2000-luvun alussa, jos kohta ei niin pahasti kuin eksponentiaalisen kasvun mallin tapauksessa.
Kuvio 8. BKT:n ennuste Suomelle vuosien 1950–2002 datan perusteella
Kuvio 9. Kokonaistuottavuuden ennuste Suomelle vuosien 1890–2002 datan perusteella
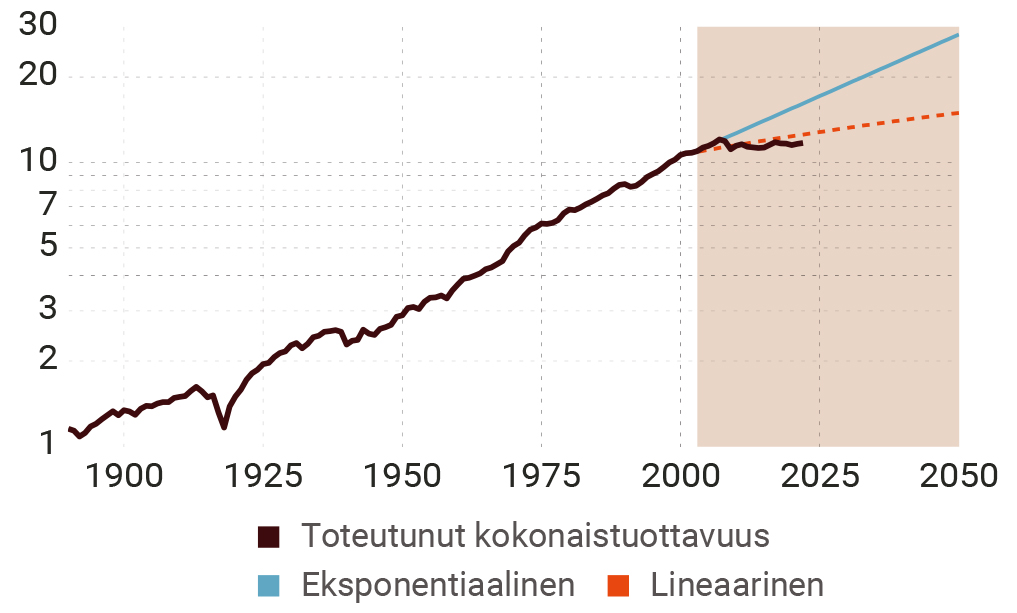
Kuvio 10. Kokonaistuottavuuden ennuste Suomelle vuosien 1950–2002 datan perusteella
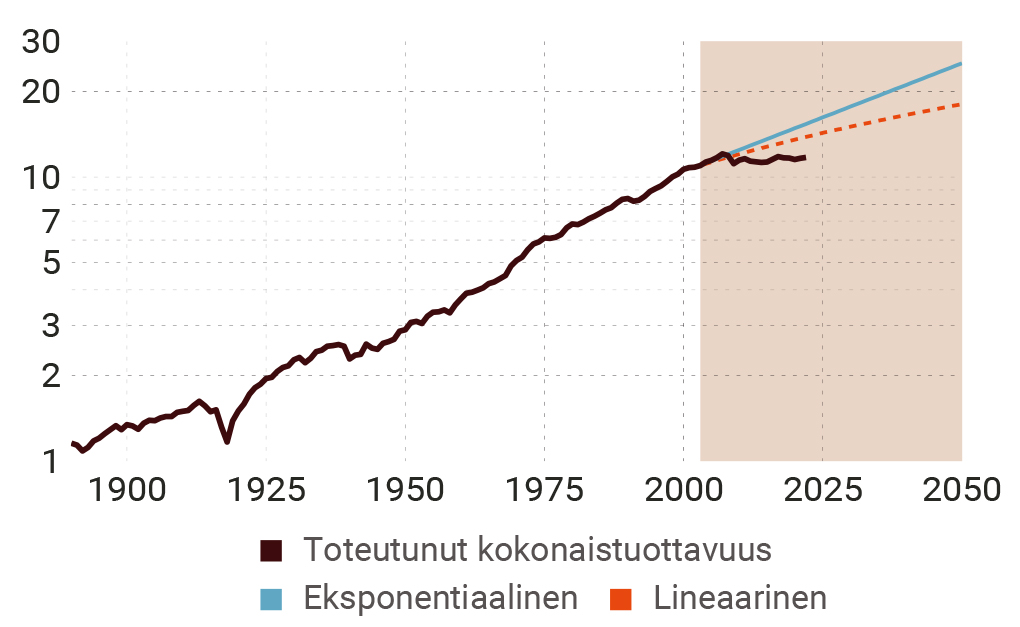
Erot näkyvät luonnollisesti ennusteluvuissa. Jos otosajanjakso on 1860–2002, BKT:n ennustettu kasvu vuonna 2050 on 2,0 prosenttia eksponentiaalisen kasvun mallissa, mutta lineaarisen kasvun mallissa vain 0,6 prosenttia. Jos otosajanjaksoksi valitaan 1950–2002, vastaavat luvut ovat 3,2 ja 1,1 prosenttia. Kokonaistuottavuuden osalta luvut noudattavat samaa kaavaa, mutta ovat tietenkin astetta pienempiä, siten maksimikasvuksi jää 1,8 prosenttia, kun otosajanjakso on 1950–2002. Koska kuvioiden perusteella lineaarinen malli vaikuttaa uskottavammalta, voinee päätellä, että kokonaistuotannon kasvu tuskin yltää edes yhteen prosenttiin.
Johtopäätöksiä ja syyllisten etsintää
Pitkän aikavälin talouskasvua koskevien ennusteiden tekeminen ei ole helppoa, koska tukeutuminen aiempien vuosien talouskasvunumeroihin on hyvin uskaliasta johtuen useasta syystä. Päällimmäinen syy on siinä, että aiempien vuosien kasvua luonnehtivat useat hyvin erilaiset kasvujaksot. Tarkasteluajanjaksoa vaihtelemalla saadaan melkein mitä tahansa numeroita.
Toinen ongelma, jota tässä artikkelissa on yritetty valottaa, on kasvun perimmäinen luonne: onko kasvu jatkuvasti eksponentiaalista vai onko se ”lineaarista” siten, että tuotanto samoin kuin tuottavuus kasvavat (odotusarvomielessä) absoluuttisesti saman verran joka vuosi? Nämä kaksi vaihtoehtoista tapaa tuottavat sitä erilaisemmat kasvuprofiilit, mitä pidemmälle aika kuluu. Kolmas ongelma koskee mahdollisia kontrollimuuttujia, demografista ja teknologista kehitystä sekä instituutioiden muutoksia. Toki kyse voi olla myös muutoksista ihmisten preferensseissä, esimerkkinä vaikka syntyvyys. Ehkä vielä vaikeampi on ennustaa tekoälyn tapaisten teknologioiden vaikutusta tuotantoon puhumattakaan keksinnöistä, joita ei ole vielä tehty.
Kokonaistuotannon samoin kuin kokonaistuottavuuden kasvun hidastuminen on yleismaailmallinen ilmiö, joka koskee käytännössä kaikkia teollisuusmaita – jopa Kiinaa myöden. Suomea se ei kuitenkaan paljon lohduta, etenkin kun Suomi näyttää olevan alisuoriutuja ainakin Pohjoismaiden välisessä vertailussa.
On aiheellista kysyä, miksi näin on. Ehkä muutama lähinnä spekulatiivinen kommentti on tässä suhteessa paikallaan.
Yksi ilmeinen Suomea vaivaava ongelma on epäedullinen väestö- ja aluekehitys. Suomi on eurooppalaisittain hyvin harvaan asuttu maa, jossa on vain muutama sellainen väestökeskittymä, joka mahdollistaa suuret investointihankkeet. Todella suuria hankkeita ei kyetä tekemään lainkaan. On vaikea kuvitella, että Suomessa kyettäisiin rakentamaan esimerkiksi Hollannin Eindhovenin kaltainen massiivinen teknokeskus USA:n Piilaakson malliin.
Pääkaupunkiseudun ulkopuolella ainoat kasvukeskukset ovat yliopistokaupunkeja, joissa väestönkasvu selittyy lähinnä opiskelijoilla, mikä ei sinällään tarjoa hyviä edellytyksiä suurille teollisille investoinneille. Hajanainen aluekehitys rasittaa julkista taloutta ja siten koko kansantaloutta, mikä ainakin epäsuorasti hidastaa myös talouskasvua6. Suomi on toki muutenkin epäedullisessa asemassa koko Euroopan mittakaavassa; se on syrjässä Euroopan kasvukeskuksista ja logistisista ratkaisuista. Se taas tietää hankaluuksia ajatellen uusien yritysten sijoittumista ja toimintaa. On selvää, että niiden suhteen tarvitaan todella isoja porkkanoita ja rohkeutta kokeilla uusia houkuttimia.
Kirjoittaja haluaa kiittää Juuso Vanhalaa ja Juhana Hukkista Suomen Pankista lukemattomista yhteisistä tuttavuuskehityksen selitysyrityksistä ja Petri Böckermania Laboresta hyödyllisistä kommenteista.
MATTI VIREN
Matti Viren on taloustieteen professori (emeritus) Turun yliopistossa. Hän opiskellut Helsingin ja Chicagon yliopistoissa ja työskennellyt paitsi Turun yliopistossa myös Suomen Pankissa, ETLAssa, VATTissa ja Puolan valtiovarainministeriössä Euroopan komission neuvonantajana. Hänen julkaisutoimintansa on keskittynyt raha- ja finanssipolitiikkaan sekä kotitalouksien kulutus- ja säästämiskäyttäytymiseen.
Viitteet
1 Philippon 2022.
2 Tuotantofunktioon liittyy lukuisa joukko erilaisia vaihtoehtoisia formulointeja alkaen kysymyksestä, miten käsitellä välituotteita, mitä olettaa työvoiman ja pääomaan substituutiosta ja mihin teknisen kehityksen oletetaan ”kiinnittyvän”: työpanokseen vai pääoman vai molempiin. Kokonaistuottavuutta koskevat mittaustulokset riippuvat tietenkin kaikista näistä tekijöistä. Ks. esim. Moss et al. (2020).
3 Ks. esim. Cowen (2022), Abramowitz (1959) ja Lipsey & Carlaw (2004).
4 Jos lasketaan muuttujien (kokonaistuottavuuden tai BKT:n kasvun) ristispektrit, voidaan todeta, että voimakkain yhteneväisyys (koherenssi) on lyhyiden (2–3 vuoden) syklien osalta. Vaikuttaa siltä, että ainakin Suomen osalta pitkän aikavälin kehitys on poikennut huomattavan paljon muista maista.
5 Kasvuvauhtia mittaamme suureella 100*logaritminen differenssi, joka on approksimatiivisesti sama kuin prosenttimuutos. Kasvua sen sijaan mittaamme pelkällä differenssillä.
6 Ks. Böckerman ja Maliranta 2003 ja 2007.
Kirjallisuus
Abramowitz, M. (1959), Resource and Output Trends in the United States since 1870, NBER Occasional paper 52.
BCLD (2022), BCLD data base.
Böckerman, P. & Maliranta, M. (2007), The micro-level dynamics of regional productivity growth: The source of divergence in Finland, Regional Science and Urban Economics 37(2), 165–182.
Böckerman, P. & Maliranta, M. (2003), Tehoton mikrotason dynamiikka. Uusi näkökulma aluetalouksien ongelmiin, Kansantaloudellinen aikakauskirja 99(2), 138–147.
Cowen, T. (2022), Additive growth, Marginal Revolution -blogi.
Perfecty, R. & Carlaw, K. (2004), Total factor productivity and the measurement of technological change, Canadian Journal of Economics, 37(4), 1118–1150.
Moss, E., Nunn, R. & Shambaugh, J. (2020), The Slowdown in Productivity Growth and Policies That Can Restore It. Hamilton project framing paper, Brookings.
Philippon, T. (2022), Additive growth, NBER Working Paper 29950.
